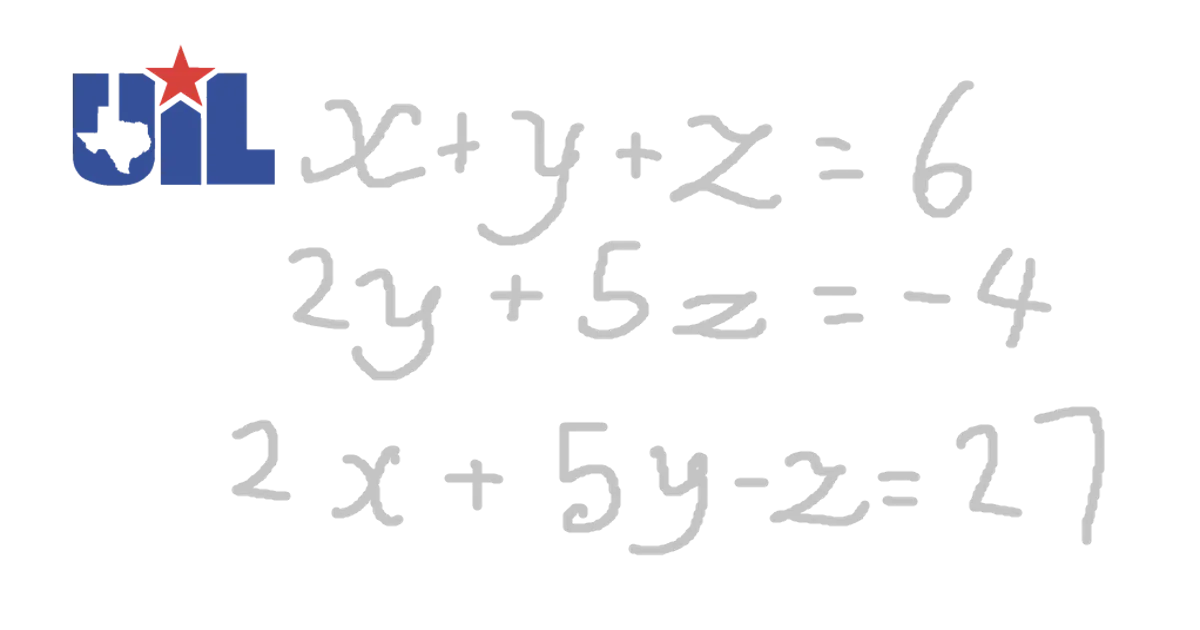UIL State CS Packet #7

I’ve been doing UIL practice to grind ~~definitely not because I was forced to~~ for state/regional. Recently I came across last year’s (2022) state packet, and I wanted to share my solutions to one of the problems.

Anyway’s let’s just get into it.

Problem statement

The problem statement is as follows:

Input consists of a single integer T, followed by T test cases.
For each test case, there will be an integer N, followed by N lines of input.
The N following lines define a system of linear equations in N variables.
All coefficients and the final constant are integers.
We need to solve the system of linear equations, and output the solution.

While the problem seems pretty straightforward, there’s a few caveats:

First of all, take a look at this example input:

3
1x+1y+1z=6
0x+2y+5z=-4
2x+5y-1z=27

We’re given the system of linear equations as pure strings, and it’s our job to parse every coefficient, variable name, and constant.

Thankfully, the input also tells us:

Variables are guarenteed to be a single lowercase letter from a - z.
Variables stay in the same order for all equations per test case.
Variables are not allowed to be the same and are not allowed to be duplicated within the same test case.`

Another caveat is the output. We have to output in the format var1=NUM1,var2=NUM2..., where NUMi is the solution for the variable vari rounded to 3 decimal places.

But first let’s worry about parsing the actual equations

Parsing input

A neat trick we can do is to use regex to parse the input. As we know the variables are lowercase letters, we can single them out like this:

// ignore the Object[] return for now
public static Object[] parseInputs(String line, int n){ // line is equation as string, n is number of variables
    String[] vars = new String[n];
 
    ArrayList<String> temp = new ArrayList<String>(Arrays.asList(line.split("[^a-z]")));
    temp.removeIf(s -> s.equals("")); 
    vars = temp.toArray(vars);
}

First, we split on every character that isn’t a lowercase letter. This gives us an array of strings, where each string is either a variable or an empty string. We can then filter out the empty strings with the cool removeIf method, and we’re left with just the variables.

For example:

"0x+2y+5z=-4" -> ["", "x", "", "y", "", "z", ""]

Filtering out s -> s.equals("") gives
["x", "y", "z"]

Now that we have the variables, let’s split on every character that IS a lowercase letter, as well as = to seperate the coefficients and constant.

We’ll store them in double[] for now because we know our final answer eventually becomes a float anyway, but we can use Integer.parseInt because we know every coefficient and constant is an integer.

public static Object[] parseInputs(String line, int n){ 
    double[] left = new double[n];
    double ret = 0;
    String[] vars = new String[n];
 
    ArrayList<String> temp = new ArrayList<String>(Arrays.asList(line.split("[^a-z]")));
    temp.removeIf(s -> s.equals("")); 
    vars = temp.toArray(vars);
    
    temp = new ArrayList<String>(Arrays.asList(line.split("[a-z=]")));
    temp.removeIf(s -> s.equals(""));
    String[] eq = temp.toArray(new String[0]); 
 
    for(int i=0;i<n;i++){
        left[i] = Integer.parseInt(eq[i]); 
    }
    ret = Integer.parseInt(eq[n]);
    return new Object[]{left, ret, vars}; // unpack later
}

Here’s an example of what this does:

"0x+2y+5z=-4" -> ["0", "+2", "+5", "", "-4"]

Filtering out s -> s.equals("") gives
["0", "+2", "+5", "-4"]

Finally casting to int gives
left = [0, 2, 5]
ret = -4

Now that we have every piece of data extracted, let’s see how we can actually solve the system of linear equations.

Linear equations and linear algebra

Let’s first take a step back and consider the set of linear equations purely mathematically.

\begin{align*} x + y + z &= 6 \newline 2y + 5z &= -4 \newline 2x + 5y - z &= 27 \end{align*}

We can represent this system of linear equations as a product of a matrix and a vector:

\begin{bmatrix} 1 & 1 & 1 \newline 0 & 2 & 5 \newline 2 & 5 & -1 \end{bmatrix} \begin{bmatrix} x \newline y \newline z \end{bmatrix}= \begin{bmatrix} 6 \newline -4 \newline 27 \end{bmatrix}

This is because if we expand out the matrix multiplication, we get our original system of linear equations.

\begin{bmatrix} 1 & 1 & 1 \newline 0 & 2 & 5 \newline 2 & 5 & -1 \end{bmatrix} \begin{bmatrix} x \newline y \newline z \end{bmatrix}= \begin{bmatrix} 1x + 1y + 1z \newline 0x + 2y + 5z \newline 2x + 5y - z \end{bmatrix}= \begin{bmatrix} x + y + z \newline 2y + 5z \newline 2x + 5y - z \end{bmatrix}= \begin{bmatrix} 6 \newline -4 \newline 27 \end{bmatrix}

However, we can also reverse this multiplication to solve for the vector of variables.

\begin{bmatrix} 1 & 1 & 1 \newline 0 & 2 & 5 \newline 2 & 5 & -1 \end{bmatrix} ^{-1} \begin{bmatrix} 6 \newline -4 \newline 27 \end{bmatrix}= \begin{bmatrix} x \newline y \newline z \end{bmatrix}

But how do we go about implementing this in Java?

Implementation (Java boilerplate ahead ⚠️)

Since we know the size of the matrix is either 2x2 or 3x3, we can just hardcode the matrix inverse for each case.

I followed the algorithms shown here, and implemented them in Java.

First let’s start with the base boilerplate code:

class Matrix {
    int size;
    double[][] mat;
 
    public Matrix(int size){
        this.size = size;
        mat = new double[size][size];
    }
    public Matrix(double[][] mat){
        this.mat = mat;
        this.size = mat.length;
    }
 
 
    public String toString(){
        String ret = "";
        for(int i=0;i<size;i++){
            for(int j=0;j<size;j++){
                ret += mat[i][j] + " ";
            }
            ret += "\n";
        }
        return ret;
    }
}

Let’s also define a method for transposing a matrix (i.e. swapping rows and columns). It’s used for inverting a 3x3 matrix.

    public Matrix transpose(){
        Matrix ret = new Matrix(size);
        for(int i=0;i<size;i++){
            for(int j=0;j<size;j++){
                ret.mat[i][j] = mat[j][i];
            }
        }
        return ret;
    }

Now let’s define a method for calculating the determinant. Again, we hardcode both sizes seperately, and also introduce a helper function for 3x3 matrices.

    public double _subdet(int i, int j){
        // only for 3x3
        // find determinant of overall matrix without row i and column j
        double[][] submat = new double[2][2];
        int k = 0;
        for(int a=0;a<3;a++){
            if (a == i) continue;
            int l = 0;
            for(int b=0;b<3;b++){
                if (b == j) continue;
                submat[k][l] = mat[a][b];
                l++;
            }
            k++;
        }
        return new Matrix(submat).det();
    }
 
    public double det(){
        if (size == 2){
            return mat[0][0]*mat[1][1] - mat[0][1]*mat[1][0];
        }
        else if (size == 3){
            double ret = 0;
            for(int i=0;i<3;i++){
                ret += mat[0][i] * _subdet(0, i) * (i%2==0 ? 1:-1); // aA - bB + cC
            }
            return ret;
        }
        return 0;
    }

A 2x2 inverse is easy to calculate:

        if (size == 2){
            double det = det();
            double[][] inv = new double[][] {{mat[1][1], -mat[0][1]}, {-mat[1][0], mat[0][0]}};
            for(int i=0;i<2;i++){
                for(int j=0;j<2;j++){
                    inv[i][j] /= det;
                }
            }
            return new Matrix(inv);
        }

which is the implemation of this formula:

\textbf{A}^{-1} = \begin{bmatrix} a & b \newline c & d \end{bmatrix}^{-1} = \frac{1}{\text{det}(\textbf{A})} \begin{bmatrix} d & -b \newline -c & a \end{bmatrix} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \newline -c & a \end{bmatrix}

But 3x3 requires a bit more work…

3x3 matrix inverse

Here’s the formula for a 3x3 matrix inverse:

\textbf{A}^{-1} = \begin{bmatrix} a & b & c \newline d & e & f \newline g & h & i \end{bmatrix}^{-1} = \frac{1}{\text{det}(\textbf{A})} \begin{bmatrix} A & B & C \newline D & E & F \newline G & H & I \end{bmatrix} ^ T = \frac{1}{\text{det}(\textbf{A})} \begin{bmatrix} A & D & G \newline B & E & H \newline C & F & I \end{bmatrix}

where

\begin{align*} &A =& \text{det} \begin{bmatrix} e & f \newline h & i \end{bmatrix}, \quad &D =& -\text{det} \begin{bmatrix} b & c \newline h & i \end{bmatrix},\quad &G =& \text{det} \begin{bmatrix} b & c \newline e & f \end{bmatrix} \newline &B =& -\text{det} \begin{bmatrix} d & f \newline g & i \end{bmatrix}, \quad &E =& \text{det} \begin{bmatrix} a & c \newline g & i \end{bmatrix},\quad &H =& -\text{det} \begin{bmatrix} a & c \newline d & f \end{bmatrix} \newline &C =& \text{det} \begin{bmatrix} d & e \newline g & h \end{bmatrix}, \quad &F =& -\text{det} \begin{bmatrix} a & b \newline g & h \end{bmatrix},\quad &I =& \text{det} \begin{bmatrix} a & b \newline d & e \end{bmatrix} \end{align*}

Thankfully, the _subdet function from earlier can also help us calculate each of these smaller determinants. This gives us final code which looks like:

        else if (size == 3){
            double det = det();
            double[][] inv = new double[3][3];
            for(int i=0;i<3;i++){
                for(int j=0;j<3;j++){
                    inv[i][j] = _subdet(i, j);
                    if ((i+j)%2 == 1) inv[i][j] *= -1;
                }
            }
            Matrix ret = new Matrix(inv);
            ret = ret.transpose();
            for(int i=0;i<3;i++){
                for(int j=0;j<3;j++){
                    ret.mat[i][j] /= det;
                }
            }
            return ret;
        }

Actually not too bad!

All together, we also need a final method to calculate the product of a matrix and a vector. This is so that we can multiply our inverted matrix by the vector of constants to finally get the solution for each variable.

    public double[] multiply_vector(double[] vec){
        assert vec.length == size;
        double[] ret = new double[size];
        for(int i=0;i<size;i++){
            for(int j=0;j<size;j++){
                ret[i] += mat[i][j] * vec[j];
            }
        }
        return ret;
    }

Putting it all together

So overall, our final process looks like this:

for each test case:
    read in n
    coefs = double[n][n]
    constants = double[n]
    vars = string[n]

    for each equation:
        read in equation
        coef, cnst, vars = parseInputs(equation, n)
        coefs[i] = coef
        constants[i] = cnst
        vars = vars         # we override each time, but it doesn't matter because vars stay in same order and place each equation

    mat = Matrix(coefs)
    inv = mat.inverse()
    solution = inv.multiply_vector(constants)

    print out formatted solution

This should work regardless of 2 or 3 variables, because we have different code for each case.

My final code for this problem looks like this:

import java.util.*;
import java.io.*;
 
public class Manuel {
    public static Object[] parseInputs(String line, int n) {
        double[] left = new double[n];
        int ret = 0;
        String[] vars = new String[n];
 
        ArrayList<String> temp = new ArrayList<String>(Arrays.asList(line.split("[^a-z]")));
        temp.removeIf(s -> s.equals(""));
        vars = temp.toArray(vars);
 
        temp = new ArrayList<String>(Arrays.asList(line.split("[a-z=]")));
        temp.removeIf(s -> s.equals(""));
        String[] eq = temp.toArray(new String[0]);
 
        for (int i = 0; i < n; i++) {
            left[i] = Integer.parseInt(eq[i]);
        }
        ret = Integer.parseInt(eq[n]);
        return new Object[] { left, ret, vars };
    }
 
    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int N = Integer.parseInt(sc.nextLine());
        for (int I = 1; I <= N; I++) { // I for Testcase #
            int n = Integer.parseInt(sc.nextLine());
            double[][] coef = new double[n][n];
            double[] res = new double[n];
            String[] vars = new String[n];
            for (int i = 0; i < n; i++) {
                Object[] ret = parseInputs(sc.nextLine(), n);
                coef[i] = (double[]) ret[0];
                res[i] = (int) ret[1];
                vars = (String[]) ret[2];
            }
 
            // System.out.println(Arrays.deepToString(coef));
            // System.out.println(Arrays.toString(res));
            // System.out.println(Arrays.toString(vars));
            Matrix mat = new Matrix(coef);
            mat = mat.inverse();
            double[] ans = mat.multiply_vector(res);
            // System.out.println(Arrays.toString(ans));
 
            // stupid weird -0.000 reduction
            for (int i = 0; i < n; i++) {
                if (Math.abs(ans[i]) < 1e-4)
                    ans[i] = 0;
            }
 
            for (int i = 0; i < n; i++) {
                System.out.printf("%s=%.3f", vars[i], ans[i]);
                if (i != n - 1)
                    System.out.print(",");
            }
            System.out.println();
        }
        sc.close();
    }
}
 
class Matrix {
    int size;
    double[][] mat;
 
    public Matrix(int size) {
        this.size = size;
        mat = new double[size][size];
    }
 
    public Matrix(double[][] mat) {
        this.mat = mat;
        this.size = mat.length;
    }
 
    public Matrix transpose() {
        Matrix ret = new Matrix(size);
        for (int i = 0; i < size; i++) {
            for (int j = 0; j < size; j++) {
                ret.mat[i][j] = mat[j][i];
            }
        }
        return ret;
    }
 
    public double _subdet(int i, int j) {
        // only for 3x3
        // find determinant of overall matrix without row i and column j
        double[][] submat = new double[2][2];
        int k = 0;
        for (int a = 0; a < 3; a++) {
            if (a == i)
                continue;
            int l = 0;
            for (int b = 0; b < 3; b++) {
                if (b == j)
                    continue;
                submat[k][l] = mat[a][b];
                l++;
            }
            k++;
        }
        return new Matrix(submat).det();
    }
 
    public double det() {
        // size only 2 or 3
        if (size == 2) {
            return mat[0][0] * mat[1][1] - mat[0][1] * mat[1][0];
        } else if (size == 3) {
            double ret = 0;
            for (int i = 0; i < 3; i++) {
                ret += mat[0][i] * _subdet(0, i) * (i % 2 == 0 ? 1 : -1); // aA - bB + cC
            }
            return ret;
        }
        return 0;
    }
 
    public Matrix inverse() {
        if (size == 2) {
            double det = det();
            double[][] inv = new double[][] { { mat[1][1], -mat[0][1] }, { -mat[1][0], mat[0][0] } };
            for (int i = 0; i < 2; i++) {
                for (int j = 0; j < 2; j++) {
                    inv[i][j] /= det;
                }
            }
            return new Matrix(inv);
        } else if (size == 3) {
            double det = det();
            double[][] inv = new double[3][3];
            for (int i = 0; i < 3; i++) {
                for (int j = 0; j < 3; j++) {
                    inv[i][j] = _subdet(i, j);
                    if ((i + j) % 2 == 1)
                        inv[i][j] *= -1;
                }
            }
            Matrix ret = new Matrix(inv);
            ret = ret.transpose();
            for (int i = 0; i < 3; i++) {
                for (int j = 0; j < 3; j++) {
                    ret.mat[i][j] /= det;
                }
            }
            return ret;
        }
        return null; // bad size
    }
 
    public double[] multiply_vector(double[] vec) {
        assert vec.length == size;
        double[] ret = new double[size];
        for (int i = 0; i < size; i++) {
            for (int j = 0; j < size; j++) {
                ret[i] += mat[i][j] * vec[j];
            }
        }
        return ret;
    }
 
    public String toString() {
        String ret = "";
        for (int i = 0; i < size; i++) {
            for (int j = 0; j < size; j++) {
                ret += mat[i][j] + " ";
            }
            ret += "\n";
        }
        return ret;
    }
}

I do have this small tidbit before printing

            for (int i = 0; i < n; i++) {
                if (Math.abs(ans[i]) < 1e-4)
                    ans[i] = 0;
            }

This is because sometimes the float multiplication isn’t entirely accurate and might cause the printf to output something like -0.000, which this code fixes.

Conclusion

There are also a few other ways to solve this problem, including Gaussian Elimination, but I chose to do it this way because it’s very generalizable and you don’t have to worry about weird row operations. I hope this writeup helped you understand this method and hopefully you’ll be able to use it in the future.

If you have any questions or suggestions, feel free to DM me on discord. Thanks for reading!