
UIUCTF 2024 Writeups
How’s it been? Recently, I played UIUCTF with Project Sekai instead of ARESx, but I was also at DiceCTF Finals on vacation, so I didn’t get much done. Still, I managed to solve a few of the misc and rev challenges, so here are their writeups.
Misc
I helped in solving astea and push and pickle as well, but since I didn’t fully solve them, I won’t be covering them here.
Slot Machine
453 Passengers / 76 Solves Author: Jake
We have onboard entertainment! Try your luck on our newly installed slot machine.
ncat --ssl slot-machine.chal.uiuc.tf 1337
We have one attachment, a simple chal.py:
chal.py
from hashlib import sha256
hex_alpha = "0123456789abcdef"
print("== Welcome to the onboard slot machine! ==")
print("If all the slots match, you win!")
print("We believe in skill over luck, so you can choose the number of slots.")
print("We'll even let you pick your lucky number (little endian)!")
lucky_number = input("What's your lucky (hex) number: ").lower().strip()
lucky_number = lucky_number.rjust(len(lucky_number) + len(lucky_number) % 2, "0")
if not all(c in hex_alpha for c in lucky_number):
print("Hey! That's not a hex number! -999 luck!")
exit(1)
hash = sha256(bytes.fromhex(lucky_number)[::-1]).digest()[::-1].hex()
length = min(32, int(input("How lucky are you feeling today? Enter the number of slots: ")))
print("=" * (length * 4 + 1))
print("|", end="")
for c in hash[:length]:
print(f" {hex_alpha[hex_alpha.index(c) - 1]} |", end="")
print("\n|", end="")
for c in hash[:length]:
print(f" {c} |", end="")
print("\n|", end="")
for c in hash[:length]:
print(f" {hex_alpha[hex_alpha.index(c) - 15]} |", end="")
print("\n" + "=" * (length * 4 + 1))
if len(set(hash[:length])) == 1:
print("Congratulations! You've won:")
flag = open("flag.txt").read()
print(flag[:min(len(flag), length)])
else:
print("Better luck next time!")There’s a lot of messy logic in here we can ignore, but the main thing is that we control some input that is sha256 hashed, then the trailing hex digits are used to determine if we “win” the slot machine.
So, the goal is to find some input that creates a hash with a lot of the same trailing hex digits. We can deal with the encoding issues later, but for now, we need to find some hash that satisfies this.
The first thing that came to mind for me was Bitcoin hashes. Bitcoin hashes are SHA256 hashes that have a lot of leading zeros, which in this case, means a lot of trailing zeros.
Fortunately, a quick google search shows us quite a few hashes with lots of 0s here.
We can take this known block with 24 zeroes, extract the block like so, and then send it over to the server for 24 characters of the flag. As it turns out, this is enough!
curl 'https://blockchain.info/rawblock/756951?format=hex' | head -c 160 > block.txtsolve.py
from pwn import remote
from hashlib import sha256
from base64 import b64decode
from Crypto.Util.number import long_to_bytes, bytes_to_long
def send_data(hash, n):
# ncat --ssl slot-machine.chal.uiuc.tf 1337
r = remote("slot-machine.chal.uiuc.tf", 1337, ssl=True)
r.sendline(hash)
r.sendline(str(n).encode())
print(r.recvall())
k = open('block.txt').read()
k = bytes.fromhex(k)
hash = sha256(sha256(k).digest()).digest().hex()
n = 24
print(hash, set(hash[-n:]))
send_data(sha256(k).hexdigest(), n)(Unfortunately I don’t remember what the flag was and remote is down, but this does get the flag)
Rev
Summarize
381 Passengers / 161 Solves Author: Nikhil
All you have to do is find six numbers. How hard can that be?
Chucking into a decomplier, we see a pretty simple main function that reads in 6 numbers and passes them into a checker.
int32_t main(int32_t argc, char** argv, char** envp) {
int32_t argc_1 = argc;
void* fsbase;
int64_t rax = *(uint64_t*)((char*)fsbase + 0x28);
puts("To get the flag, you must correc…");
putchar(0xa);
printf("a = ");
uint32_t var_60;
__isoc99_scanf("%d", &var_60);
printf("b = ");
uint32_t var_5c;
__isoc99_scanf("%d", &var_5c);
printf("c = ");
uint32_t var_58;
__isoc99_scanf("%d", &var_58);
printf("d = ");
uint32_t var_54;
__isoc99_scanf("%d", &var_54);
printf("e = ");
uint32_t var_50;
__isoc99_scanf("%d", &var_50);
printf("f = ");
uint32_t var_4c;
__isoc99_scanf("%d", &var_4c);
if (sub_40137b(var_60, var_5c, var_58, var_54, var_50, var_4c) == 0)
puts("Wrong.");
else
{
puts("Correct.");
void var_48;
sprintf(&var_48, "uiuctf{%x%x%x%x%x%x}", ((uint64_t)var_60), ((uint64_t)var_5c), ((uint64_t)var_58), ((uint64_t)var_54), ((uint64_t)var_50), ((uint64_t)var_4c), argv);
puts(&var_48);
}
*(uint64_t*)((char*)fsbase + 0x28);
if (rax == *(uint64_t*)((char*)fsbase + 0x28))
return 0;
__stack_chk_fail();
/* no return */
}The checker seems simple as well, we have a range check and then a final check at the end.
uint64_t sub_40137b(uint32_t arg1, uint32_t arg2, uint32_t arg3, uint32_t arg4, uint32_t arg5, uint32_t arg6) {
if ((arg1 <= 100000000 || (arg2 <= 100000000 || (arg3 <= 100000000 || (arg4 <= 100000000 || (arg5 <= 100000000 || arg6 <= 100000000))))))
return 0;
if ((arg1 > 999999999 || (arg2 > 999999999 || (arg3 > 999999999 || (arg4 > 999999999 || (arg5 > 999999999 || arg6 > 999999999))))))
return 0;
int32_t rax_4 = sub_40163d(sub_4016d8(arg1, arg2), arg3);
int32_t rax_15 = sub_40163d(arg1, arg2);
int32_t rax_22 = sub_4016fe(2, arg2);
int32_t rax_71;
if (((((((((rax_4 % 17492321) != 0x3f29b9 || (rax_15 % 0x1093a1d) != 0x8bdcd2) || (COMBINE(0, sub_4016d8(sub_4016fe(3, arg1), rax_22)) % sub_40174a(arg1, arg4)) != 0x212c944d) || (sub_4017a9(arg2, sub_40163d(arg3, arg1)) % 0x6e22) != 0x31be) || (COMBINE(0, sub_40163d(arg2, arg4)) % arg1) != 0x2038c43c) || (sub_40174a(arg3, sub_40163d(arg4, arg6)) % 0x1ce628) != 0x1386e2) || (sub_4016d8(arg5, arg6) % 0x1172502) != 0x103cf4f) || (sub_40163d(arg5, arg6) % 0x2e16f83) != 0x16ab0d7))
rax_71 = 0;
else
rax_71 = 1;
return ((uint64_t)(rax_71 & 1));
}The goal here is to figure out what each inner function does, then we can write a Z3 script to solve for the 6 numbers and get the flag.
Inner functions
Let’s start from the top.
This function accepts 2 numbers, then does some bitwise operations. var_1c seems to be some counter for the number of bits, leaving var_20 as the carry, and var_10 as the result.
Clearly, this must be addition. Every bit, we add the XOR of the bits and the carry, then shift it over by the counter. The carry is updated by the OR of the ANDs of the bits and the carry. Finally, we add any remaining carry.
int64_t sub_40163d(uint32_t arg1, uint32_t arg2) __pure {
uint32_t var_2c = arg1;
uint32_t var_30 = arg2;
int64_t var_10 = 0;
int32_t var_20 = 0;
int32_t var_1c = 0;
while ((var_2c != 0 || var_30 != 0))
{
int32_t rax_2 = (var_2c & 1);
int32_t rax_4 = (var_30 & 1);
var_2c u>>= 1;
var_30 u>>= 1;
var_10 += ((uint64_t)(((rax_2 ^ rax_4) ^ var_20) << var_1c));
var_20 = ((rax_4 & var_20) | ((rax_2 & rax_4) | (rax_2 & var_20)));
var_1c += 1;
}
return (var_10 + (((uint64_t)var_20) << var_1c));
}If sub_40163d is addition, then this is subtraction. We can see that the second argument is negated, then passed into sub_40163d.
int64_t sub_4016d8(uint32_t arg1, int32_t arg2) {
return sub_40163d(arg1, -(arg2));
}For every bit in arg1, we multiply arg2 by the bit and shift it over by the counter. This is multiplication.
uint64_t sub_4016fe(uint32_t arg1, int32_t arg2) __pure {
uint32_t i = arg1;
int32_t var_14 = 0;
int32_t var_10 = 0;
while (i != 0)
{
var_14 += ((arg2 << var_10) * (i & 1));
i u>>= 1;
var_10 += 1;
}
return ((uint64_t)var_14);
}This is similar to addition, but this time there is no carry, only the XOR of the bits. This is XOR.
uint64_t sub_40174a(uint32_t arg1, uint32_t arg2) __pure {
uint32_t var_1c = arg1;
uint32_t var_20 = arg2;
int32_t var_18 = 0;
int32_t var_14 = 0;
while ((var_1c != 0 || var_20 != 0))
{
int32_t rax_2 = (var_1c & 1);
int32_t rax_4 = (var_20 & 1);
var_1c u>>= 1;
var_20 u>>= 1;
var_18 += ((rax_2 ^ rax_4) << var_14);
var_14 += 1;
}
return ((uint64_t)var_18);
}This is just like XOR, but this time we only add the AND of the bits. This is AND.
uint64_t sub_4017a9(uint32_t arg1, uint32_t arg2) __pure {
uint32_t var_1c = arg1;
uint32_t var_20 = arg2;
int32_t var_18 = 0;
int32_t var_14 = 0;
while ((var_1c != 0 || var_20 != 0))
{
int32_t rax_2 = (var_1c & 1);
int32_t rax_4 = (var_20 & 1);
var_1c u>>= 1;
var_20 u>>= 1;
var_18 += ((rax_2 & rax_4) << var_14);
var_14 += 1;
}
return ((uint64_t)var_18);
}Finally, renaming all the functions, we can see what the checker really looks like:
uint64_t check(uint32_t arg1, uint32_t arg2, uint32_t arg3, uint32_t arg4, uint32_t arg5, uint32_t arg6) {
if ((arg1 <= 100000000 || (arg2 <= 100000000 || (arg3 <= 100000000 || (arg4 <= 100000000 || (arg5 <= 100000000 || arg6 <= 100000000))))))
return 0;
if ((arg1 > 999999999 || (arg2 > 999999999 || (arg3 > 999999999 || (arg4 > 999999999 || (arg5 > 999999999 || arg6 > 999999999))))))
return 0;
int32_t rax_4 = add(sub(arg1, arg2), arg3);
int32_t rax_15 = add(arg1, arg2);
int32_t rax_22 = mul(2, arg2);
int32_t rax_71;
if (((((((((rax_4 % 17492321) != 0x3f29b9 || (rax_15 % 0x1093a1d) != 0x8bdcd2) || (COMBINE(0, sub(mul(3, arg1), rax_22)) % xor(arg1, arg4)) != 0x212c944d) || (and(arg2, add(arg3, arg1)) % 0x6e22) != 0x31be) || (COMBINE(0, add(arg2, arg4)) % arg1) != 0x2038c43c) || (xor(arg3, add(arg4, arg6)) % 0x1ce628) != 0x1386e2) || (sub(arg5, arg6) % 0x1172502) != 0x103cf4f) || (add(arg5, arg6) % 0x2e16f83) != 0x16ab0d7))
rax_71 = 0;
else
rax_71 = 1;
return ((uint64_t)(rax_71 & 1));
}Z3 Script
Now that we know what each function does, we can write a Z3 script to solve for the 6 numbers.
from z3 import *
inp = [BitVec('inp_%d' % i, 32) for i in range(6)]
a, b, c, d, e, f = inp
s = Solver()
# make sure all 9 digit numbers
for i in range(6):
s.add(inp[i] >= 100000000)
s.add(inp[i] <= 999999999)
v7 = a - b
v18 = (v7 + c) % 0x10AE961
v19 = (a + b) % 0x1093A1D
v8 = 2 * b
v9 = 3 * a
v10 = (v9 - v8) % (a ^ d)
v11 = c + a
v21 = (b & v11) % 0x6E22
v22 = (b + d) % a
v12 = d + f
v23 = (c ^ v12) % 0x1CE628
v24 = (e - f) % 0x1172502
v25 = (e + f) % 0x2E16F83
s.add(v18 == 4139449)
s.add(v19 == 9166034)
s.add(v10 == 556569677)
s.add(v21 == 12734)
s.add(v22 == 540591164)
s.add(v23 == 1279714)
s.add(v24 == 17026895)
s.add(v25 == 23769303)
if s.check() == sat:
m = s.model()
print([m[inp[i]].as_long() for i in range(6)])
else:
print('unsat')Running this script, we get the 6 numbers and the flag.
$ python3 summarize.py
[705965527, 780663452, 341222189, 465893239, 966221407, 217433792]
$ ./summarize
To get the flag, you must correctly enter six 9-digit positive integers: a, b, c, d, e, and f.
a = 705965527
b = 780663452
c = 341222189
d = 465893239
e = 966221407
f = 217433792
Correct.
uiuctf{2a142dd72e87fa9c1456a32d1bc4f77739975e5fcf5c6c0}Pwnymaps
483 Passengers / 30 Solves Author: spicypete
My friend gave me his address, but the coords he gave are n dimensional… Can you help me setup my GPS to find him?
Once you pass all checks, you need to plot all the x, y points in order as a line plot in order to reveal the flag. The flag consists of three valid words seperated by underscores, wrapped in the flag format, and all lowercase.
The main gimmick with this challenge is that the coordinates are stored in Morton encoding. Other than that, the rest is mostly just simple operations and checks.
Here’s Binja’s decompilation of the main function:
main.hlil
int32_t main(int32_t argc, char** argv, char** envp)
uint8_t arr[0x200][0x8]
arr[3] = arr[3]
int32_t argc_1 = argc
char** argv_1 = argv
void* fsbase
int64_t rax = *(fsbase + 0x28)
setvbuf(fp: __TMC_END__, buf: nullptr, mode: 2, size: 0)
setvbuf(fp: stdin, buf: nullptr, mode: 2, size: 0)
int64_t __saved_rbp
for (int32_t i = 0; i s<= 0x1ff; i += 1)
for (int32_t j = 0; j s<= 7; j += 1)
*((sx.q(j) << 3) - 0x10 + &__saved_rbp + sx.q(i) - 0x1010) = 0
puts(str: "*****************")
puts(str: "* PWNYMAPS v0.1 *")
puts(str: "*****************")
puts(str: "The developer has only tested no…")
printf(format: "%s", "Indicate your directional comple…")
int32_t N
__isoc99_scanf(format: "%u", &N)
getchar()
int32_t result
if (N s> 512 || N s< 0)
label_219c:
puts(str: "Continue straight for 500 meter(…")
result = 1
else
int32_t var_1068_1 = 1
for (int32_t i_1 = 0; i_1 s< N; i_1 += 1)
printf(format: "Indicate your 'Earth'-type coord…", zx.q(i_1))
int32_t X
int32_t Y
__isoc99_scanf(format: "%u%u", &X, &Y)
getchar()
if (Y u> 0xfffffff)
goto label_219c
uint32_t rax_18 = X u>> 8
int16_t rax_23 = (Y u>> 0x1c).w | ((X << 4).w & 0xff0)
uint16_t rax_25 = (Y u>> 0x10).w & 0xfff
int32_t var_1050_1 = EncodeMorton_24bit(EncodeMorton_12bit((Y u>> 0xa).b & 0x3f, (Y u>> 4).b & 0x3f), rax_25)
int64_t rax_41 = zx.q(rax_23) | EncodeMorton_48bit(rax_18, zx.d(rax_25)) << 0xc
arr[sx.q(i_1)][0] = Unpad64Bit_8Bit(rax_41)
arr[sx.q(i_1)][1] = Unpad64Bit_8Bit(rax_41 u>> 1)
arr[sx.q(i_1)][2] = Unpad64Bit_8Bit(rax_41 u>> 2)
arr[sx.q(i_1)][3] = Unpad64Bit_8Bit(rax_41 u>> 3)
arr[sx.q(i_1)][4] = Unpad64Bit_8Bit(rax_41 u>> 4)
arr[sx.q(i_1)][5] = Unpad64Bit_8Bit(rax_41 u>> 5)
arr[sx.q(i_1)][6] = Unpad64Bit_8Bit(rax_41 u>> 6)
arr[sx.q(i_1)][7] = Unpad64Bit_8Bit(rax_41 u>> 7)
char rax_67 = arr[sx.q(i_1)][1]
arr[sx.q(i_1)][1] = arr[sx.q(i_1)][5]
arr[sx.q(i_1)][5] = rax_67
uint16_t rdx_27 = ((zx.d(arr[sx.q(i_1)][0]) << 8).w | zx.w(arr[sx.q(i_1)][1])) ^ (zx.w(arr[sx.q(i_1)][3]) | (zx.d(arr[sx.q(i_1)][2]) << 8).w)
uint16_t rax_113 = (zx.w(arr[sx.q(i_1)][7]) | (zx.d(arr[sx.q(i_1)][6]) << 8).w) ^ rdx_27 ^ (zx.w(arr[sx.q(i_1)][5]) | (zx.d(arr[sx.q(i_1)][4]) << 8).w)
int32_t rax_115 = numberOfSetBits(zx.d(rax_113))
if (correct_checksums[sx.q(i_1)] != hash(rax_115))
var_1068_1 = 0
if (var_1068_1 == 0)
goto label_219c
for (int32_t i_2 = 1; i_2 s< N; i_2 += 1)
for (int32_t j_1 = 0; j_1 s<= 7; j_1 += 1)
*((sx.q(i_2) << 3) - 0x10 + &__saved_rbp + sx.q(j_1) - 0x1010) ^= (numberOfSetBits(zx.d(*((sx.q(i_2 - 1) << 3) - 0x10 + &__saved_rbp + sx.q(j_1) - 0x1010))) << 8).b
for (int32_t i_3 = 0; i_3 s< N; i_3 += 1)
char rdx_36 = ((zx.d(arr[sx.q(i_3)][1]) s>> 1).b & 0x40) | ((zx.d(arr[sx.q(i_3)][2]) s>> 2).b & 0x20) | ((zx.d(arr[sx.q(i_3)][3]) s>> 3).b & 0x10) | ((zx.d(arr[sx.q(i_3)][4]) s>> 4).b & 8)
int64_t rax_247 = EncodeMorton_9x7bit(arr[sx.q(i_3)][0] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][1] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][2] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][3] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][4] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][5] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][6] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][7] & 0x7f, arr[sx.q(i_3)][7] u>> 7 | rdx_36 | ((zx.d(arr[sx.q(i_3)][5]) s>> 5).b & 4) | ((zx.d(arr[sx.q(i_3)][6]) s>> 6).b & 2))
if ((rax_247 | zx.q(arr[sx.q(i_3)][0] u>> 7) << 63) != correct[sx.q(i_3)])
goto label_219c
puts(str: "You have reached your destinatio…")
result = 0
*(fsbase + 0x28)
if (rax == *(fsbase + 0x28))
return result
__stack_chk_fail()
noreturnThe program reads in 512 x, y coordinates, then does some fairly simple operations, and finally checks each number in two ways.
First, it checks the number of set bits by calculating a checksum given the number of set bits and ensuring it matches the stored checksum.
...
int32_t rax_115 = numberOfSetBits(zx.d(rax_113))
if (correct_checksums[sx.q(i_1)] != hash(rax_115))
var_1068_1 = 0
...
uint64_t hash(int32_t arg1) __pure
int32_t rax_3 = (arg1 u>> 0x10 ^ arg1) * 0x45d9f3b
int32_t rax_7 = (rax_3 u>> 0x10 ^ rax_3) * 0x45d9f3b
return zx.q(rax_7 ^ rax_7 u>> 0x10)Then, there is another seperate check for a calculated correct value.
for (int32_t i_3 = 0; i_3 s< N; i_3 += 1)
char rdx_36 = ((zx.d(arr[sx.q(i_3)][1]) s>> 1).b & 0x40) | ((zx.d(arr[sx.q(i_3)][2]) s>> 2).b & 0x20) | ((zx.d(arr[sx.q(i_3)][3]) s>> 3).b & 0x10) | ((zx.d(arr[sx.q(i_3)][4]) s>> 4).b & 8)
int64_t rax_247 = EncodeMorton_9x7bit(arr[sx.q(i_3)][0] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][1] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][2] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][3] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][4] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][5] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][6] & 0x7f, arr[sx.q(mods.dp.d(sx.q(i_3), N))][7] & 0x7f, arr[sx.q(i_3)][7] u>> 7 | rdx_36 | ((zx.d(arr[sx.q(i_3)][5]) s>> 5).b & 4) | ((zx.d(arr[sx.q(i_3)][6]) s>> 6).b & 2))
if ((rax_247 | zx.q(arr[sx.q(i_3)][0] u>> 7) << 63) != correct[sx.q(i_3)])
goto label_219cI won’t go into detail about the Morton encoding, you can read the previously linked article, but essentially it interweaves the bits of the stored numbers to create a single number.
To deal with this encoding, I recreated the encoding and decoding functions in the binary in Python like so:
def PadNBit(a1, n):
result = 0
for i in range(n):
result |= (a1 & (1 << i)) << i
return result
def Pad6Bit(a1):
return PadNBit(a1, 6)
def Pad12Bit(a1):
return PadNBit(a1, 12)
def EncodeMorton_12bit(x, y):
return Pad6Bit(x) | (Pad6Bit(y) << 1)
def EncodeMorton_24bit(x, y):
return Pad12Bit(x) | (Pad12Bit(y) << 1)
def EncodeMorton_48bit(x, y):
return PadNBit(x, 24) | (PadNBit(y, 24) << 1)
def Unpad64Bit_8Bit(a1):
result = 0
for i in range(7, 64, 8):
result |= (a1 & (1 << (63 - i))) >> (56 - i + i // 8)
return result
def set_bits(a1):
count = 0
for i in range(64):
count += (a1 & (1 << i)) >> i
return count
def Pad7Bit(a1):
result = 0
for i in range(7):
result |= (a1 & (1 << i)) << (8 * i)
return result
def EncodeMorton_9x7bit(a1, a2, a3, a4, a5, a6, a7, a8, a9):
return Pad7Bit(a1) | (Pad7Bit(a2) << 1) | (Pad7Bit(a3) << 2) | (Pad7Bit(a4) << 3) | (Pad7Bit(a5) << 4) | (Pad7Bit(a6) << 5) | (Pad7Bit(a7) << 6) | (Pad7Bit(a8) << 7) | (Pad7Bit(a9) << 8)I used entirely bitwise functions to ensure that these functions would also work with Z3 BitVecs.
All we have to do now is to write a Z3 script to solve for all the x, y coordinates.
solve.py
def calc_sym(_bitcount, _correct):
x, y = BitVecs('x y', 64)
# v19 = X >> 8;
# v6 = (16 * X) & 0xFF0 | (Y >> 28);
# v7 = HIWORD(Y) & 0xFFF;
# v8 = EncodeMorton_12bit((unsigned __int16)Y >> 10, (Y >> 4) & 0x3F);
# v20 = EncodeMorton_24bit(v8, v7);
# v24 = EncodeMorton_48bit(v19, v7);
# v25 = (v24 << 12) | v6;
v19 = x >> 8
v6 = ((x << 4) & 0xFF0 | (y >> 28)) & 0xFFFF
v7 = (y >> 16) & 0xFFF
v8 = EncodeMorton_12bit((y >> 10) & 0x3F, (y >> 4) & 0x3F)
v20 = EncodeMorton_24bit(v8, v7)
v24 = EncodeMorton_48bit(v19, v7)
v25 = (v24 << 12) | v6
v26 = [Unpad64Bit_8Bit(v25 >> i) for i in range(8)]
v5 = v26[1]
v26[1] = v26[5]
v26[5] = v5
# (unsigned __int16)((((unsigned __int8)v26[8 * k + 4] << 8) | (unsigned __int8)v26[8 * k + 5]) ^ (((unsigned __int8)v26[8 * k + 2] << 8) | (unsigned __int8)v26[8 * k + 3]) ^ ((unsigned __int8)v26[8 * k + 1] | ((unsigned __int8)v26[8 * k] << 8)) ^ (((unsigned __int8)v26[8 * k + 6] << 8) | (unsigned __int8)v26[8 * k + 7]))
v27 = (((v26[4] & 0xff) << 8) | (v26[5] & 0xff)) ^ (((v26[2] & 0xff) << 8) | (v26[3] & 0xff)) ^ ((v26[1] & 0xff) | ((v26[0] & 0xff) << 8)) ^ (((v26[6] & 0xff) << 8) | (v26[7] & 0xff)) & 0xffff
bitcount = set_bits(v27)
# ((int)(unsigned __int8)v26[8 * ii + 6] >> 6) & 2 | ((int)(unsigned __int8)v26[8 * ii + 5] >> 5) & 4 | ((int)(unsigned __int8)v26[8 * ii + 4] >> 4) & 8 | ((int)(unsigned __int8)v26[8 * ii + 3] >> 3) & 0x10 | ((int)(unsigned __int8)v26[8 * ii + 2] >> 2) & 0x20 | ((int)(unsigned __int8)v26[8 * ii + 1] >> 1) & 0x40u | ((unsigned __int8)v26[8 * ii + 7] >> 7));
tmp = ((v26[6] >> 6) & 2) | ((v26[5] >> 5) & 4) | ((v26[4] >> 4) & 8) | ((v26[3] >> 3) & 0x10) | ((v26[2] >> 2) & 0x20) | ((v26[1] >> 1) & 0x40) | (v26[7] >> 7) & 0xff
v22 = EncodeMorton_9x7bit(v26[0] & 0x7f, v26[1] & 0x7f, v26[2] & 0x7f, v26[3] & 0x7f, v26[4] & 0x7f, v26[5] & 0x7f, v26[6] & 0x7f, v26[7] & 0x7f, tmp)
v23 = (v26[0] >> 7) & 0xff
v22 |= v23 << 63
s = Solver()
s.add(ULE(x, 0xffffffff))
s.add(ULE(y, 0xffffffff))
s.add(_bitcount == bitcount)
s.add(v22 == _correct)
if s.check() == sat:
m = s.model()
# print(m[x], m[y])
return m[x].as_long(), m[y].as_long()
else:
print('unsat')Finally, we need to graph the X, Y coordinates as described in the challenge prompt.
plot.py
import matplotlib.pyplot as plt
from tqdm import tqdm
from solve import calc_sym
import struct
def hash(a):
rax_3 = (((a >> 0x10) ^ a) * 0x45d9f3b) & 0xFFFFFFFF
rax_7 = (((rax_3 >> 0x10) ^ rax_3) * 0x45d9f3b) & 0xFFFFFFFF
return (rax_7 >> 0x10) ^ rax_7
data = open('pwnymaps', 'rb').read()
inv_map = {hash(i): i for i in range(32)}
checksums = data[0x4aa0:0x4aa0+(335*4)]
checksums = [struct.unpack('<I', checksums[i:i+4])[0]
for i in range(0, len(checksums), 4)]
set_bits = [inv_map[checksum] for checksum in checksums]
print(set_bits[:10])
correct = data[0x4020:0x4020+(335*8)]
correct = [struct.unpack('<Q', correct[i:i+8])[0]
for i in range(0, len(correct), 8)]
print(correct[:10])
points = []
for bs, res in tqdm(list(zip(set_bits, correct))):
points.append(calc_sym(bs, res))
print(points)
# graph as points, draw line path
x = [p[0] for p in points]
y = [p[1] for p in points]
plt.plot(x, y)
plt.savefig('path.png')This gives us our final flag, which reads
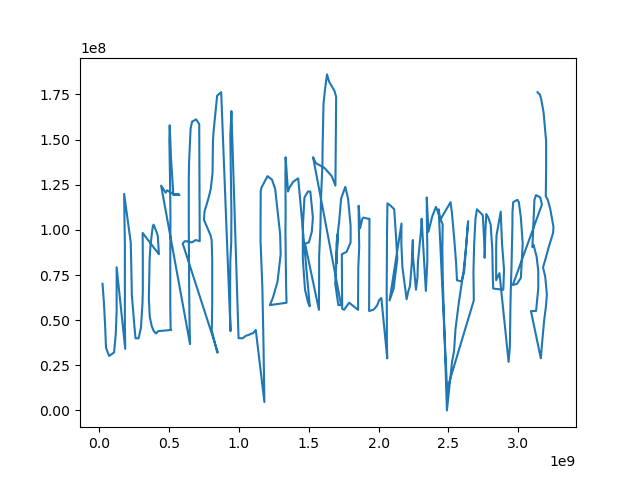
uiuctf{I_prefer_pwny_maps}.